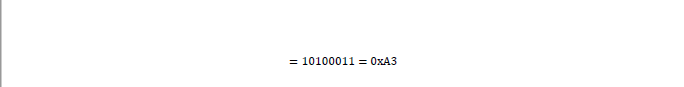这篇文章距离他上一次更新已经过去了……我算算啊……好像是 1095 天吧，不知道是否还有效啊!

攻击方法

唯密文攻击（Ciphertext Only Attack，COA）：仅持有密文。

已知明文攻击：（Known Plaintext Attack，KPA）：掌握了一些明密文对。

选择明文攻击（Chosen Plaintext Attack，CPA）：截获加密机。

选择密文攻击（Chosen Ciphertext Attack，CCA）：截获解密机。

古典密码

大写字母A~~Z和小写字母a~~z分别对应数字0~25（考试会给出表格）。

重点是置换密码：

单表：加法、乘法、仿射
多表：Playfair、Vigenere

安全性分析（包括抗暴力破解强度，即密钥空间大小）

分组密码

DES

算法过程

img

计算：S盒

查表，最高位和最低位对应行号，中间位对应列号。

安全性

互补性

弱密钥

双重、三重DES分析（加密的强度：密钥空间）

AES

算法过程（加密/解密）

解密是加密的逆过程。

计算

字节上的计算。

字节代换（S 盒）

简单的查表。

逆：也是查表。

行移位

简单的移位。

第0行不变，第1行左移1个字节，第2行左移2个字节，第3行左移3个字节。

逆：变成右移。

列混合

这应该是 AES 考察的重中之重。

加法：异或

乘法两种方法：

用定义
用简便方法（乘2情况下）
- 最高位是0：直接左移1位。
- 最高位是1：左移1位后和 00011011 异或。

乘3情况：(00000011=00000010⊕00000001)

逆：太难，不要求掌握。

轮密钥加

逐位异或。

密钥扩展

看了下书，宛若没学2333。

128 位密钥形成4个4字节组成的（32位）字：w[0],w[1],w[2],w[3]w[0],w[1],w[2],w[3] ，这是初始密钥加用到的。

扩充40个新列，以如下算法生成：

若 ii 不是4的倍数，那么 w[i]=w[i−4]⊕w[i−1]w[i]=w[i−4]⊕w[i−1] 。
若 ii 是4的倍数，那么 w[i]=w[i−4]⊕T(w[i−1])w[i]=w[i−4]⊕T(w[i−1]) 。

其中，T()T() 是一个很复杂的函数，定义如下：

字循环：循环左移一个字节，即有 [b0,b1,b2,b3]→[b1,b2,b3,b4][b0,b1,b2,b3]→[b1,b2,b3,b4] 。
字节代换：用字节代换中的 S 盒，直接查表。
轮常量异或。

工作模式

根据加密图画出解密图。

根据图写出算法。

错误传播分析。

电子密码本模式（ECB）
密码分组链接模式（CBC）
密码反馈模式（CFB）
输出反馈模式（OFB）
计数器模式（CTR）

流密码

给定初始状态，写出输出序列。线性反馈移位寄存器（LFSR）。

周期、游程分析。

本原多项式、m序列。

哈希函数

不要求掌握完整算法。

因为不考记忆算法，后面的也很难算，能考的或许只有数据填充（99.9%考）。

本身含义、安全性分析（碰撞性）。

基本概念

Hash 函数是密码学的一个重要分支，是将任意长度的输入变换为固定长度的输出的不可逆的单向密码体制。

性质

任意长度输入。
固定长度输出。
对于任意给定的消息 xx ，计算 H(x)H(x) 比较容易，硬件软件均可实现。
单向性（抗原像性）：从散列值 h=H(m)h=H(m) 推回消息 mm 在计算上不可行。
抗弱碰撞性：对任意给定的消息 xx ，找到 y≠xy≠x 且 H(x)=H(y)H(x)=H(y) 在计算上不可行。
抗强碰撞性：找到任何满足 H(x)=H(y)H(x)=H(y) 的两个不同消息 x,yx,y 在计算上不可行。

数据填充

填充一个1和若干个0，使得消息长度模 512 与 448 同余。

特别注意：若原消息长度刚好满足这个条件，则再填充 512 位（1 个 1 和 511 个 0）。

填充完后再把原始消息长度以 64 比特表示附加在后面。

这样，最终消息长度恰好为 512 的整数倍。

MD5

分组长度为 512 比特，最终输出 128 位（即 16 字节，32 个十六进制位）的消息摘要。

过程为 4 轮，每轮 16 步，共 64 步。

SHA1

最终输出 160 位（即 20 字节，40 个十六进制位）的消息摘要。（因此比 MD5 抗穷举能力更强）

过程为 4 轮，每轮 20 步，共 80 步。

看到后面的步骤，心中呐喊：打扰了。

公钥密码

相当于单向陷门函数，陷门是私钥。

RSA

算法流程（加密、解密）

计算

给出 p,q,ep,q,e 求 dd

n=p⋅q φ(n)=(p−1)⋅(q−1) d≡e−1(modφ(n))n=p⋅q φ(n)=(p−1)⋅(q−1) d≡e−1(modφ(n))

加密：给出 mm 求 cc

c≡me(modn)c≡me(modn)

解密：给出 cc 求 mm

m≡cd(modn)m≡cd(modn)

安全性分析

正确性验证

(m,e)=1(m,e)=1
(m,e)≠1(m,e)≠1

攻击与防范（肯定考）

共模攻击

低指数攻击

ElGamal

不考安全性分析。

加密解密算法（必须记住）

计算

正确性验证

数字签名

签名用私钥，验证用公钥。

RSA

ElGamal（如果考会给出算法）

特殊：盲签名

安全性分析

若不加 Hash 会怎么样？（没有Hash函数有什么缺点？）

可以伪造签名。

看P246 6.

正确性分析

密码协议

联系《密码学课程设计》的综合实验。

对称密码用到的密钥用公钥密码体制传输。

Alice 用 Bob 的公钥加密对称密码的密钥，发送给 Bob 。
Bob 用自己的私钥解密，得到密钥。

给出具体密码协议，分析合理性，验证可靠性，证明安全性。

综合，会涉及到前面学的。

一些题目

仿射密码

题目

若 ci=E(mi)=(11⋅mi+6)mod26ci=E(mi)=(11⋅mi+6)mod26：

若明文为 cumtcumt ，请计算相应的密文。
写出解密变换。
若密文文 cumtcumt，请计算相应的明文。

解答

字母-数字对应表：（考试会给出）

A	B	C	D	E	F	G	H	I	J	K	L	M	N	O	P	Q	R	S	T	U	V	W	X	Y	Z
0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25

由 ci=E(mi)=(11⋅mi+6)mod26ci=E(mi)=(11⋅mi+6)mod26

cc 对应 2，对应密文为 2，对应 cc；

uu 对应 20，对应密文为 18，对应 ss；

mm 对应12，对应密文为 8，对应 ii ；

tt 对应 19，对应密文为 1，对应 bb 。

故 cumtcumt 对应的密文为 csibcsib 。

∵11−1≡19(mod26) ∴解密变换为mi=[19⋅(y−6)]mod26∵11−1≡19(mod26) ∴解密变换为mi=[19⋅(y−6)]mod26

RSA

题目

RSA 加密算法是当前使用最为广泛的公钥加密算法。假设消息接收方选择 p=43,q=59,e=13p=43,q=59,e=13 ，请回答以下问题：

发送方预加密消息 224224 并发送给接收方，请计算密文。
请计算解密方的解密密钥 dd。
若收到的密文为 803803 ，请计算相应的明文。

解答

n=p⋅q=43⋅59=2537 φ(n)=(p−1)⋅(q−1)=42⋅58=2436 c≡me≡22413≡1692(modn) ∴密文为1692n=p⋅q=43⋅59=2537 φ(n)=(p−1)⋅(q−1)=42⋅58=2436 c≡me≡22413≡1692(modn) ∴密文为1692

使用扩展 Euclid 算法求模逆：

jj	sj−1sj−1	tj−1tj−1	qjqj	rjrj
-2				2436
-1	1	0		13
0	0	1	187	5
1	1	-187	2	3
2	-2	375	1	2
3	3	-562	1	1
4	-5	937	2	0

使用 Python 验算：

img

∴d≡e−1≡937(modφ(n))∴d≡e−1≡937(modφ(n))

若收到密文为 803803 则：

m≡cd≡803937≡1727(modn)m≡cd≡803937≡1727(modn)

即明文为 17271727 。

第一章密码学概论

信息安全（密码编码学：认证体制+保密体制）

在这里插入图片描述

1.信息安全基础概念

攻击的主要形式和分类：

在这里插入图片描述

主动攻击：

对数据流进行窜改或产生假的数据流

（1）中断(阻止)：对系统可用性进行攻击

破坏计算机硬件，网络，或文件管理系统。如DoS，病毒等

（2）篡改：对完整性进行攻击

修改文件中的数据(数据修改后存储)，替换某一程序使其执行不同功能

修改网络中传送消息的内容等，比如中间节点对转发的图象进行了压缩

（3）伪造：对真实性进行攻击
在网络中插入伪造的消息冒充消息发送者，在文件中插入伪造记录等

安全攻击的主要形式：
（1）中断

（2）截取

（3）伪造

（4）篡改

（5）重放

在这里插入图片描述

2.信息基本安全目标

保密性(Confidentiality)：确保秘密信息不向非授权者泄露
完整性(Integrity)：确保信息和程序只能以特定和授权的方式进行改变
可用性(Availability)：确保系统能工作迅速，对授权用户不能拒绝

也被称为CIA三元组，还有两个目标也经常被提及

真实性(Authenticity)：能验证该用户是否是他声称的那个人，系统的输入是否来自可信任的信源
可追溯性(Accountability)：要求实体的行为可以唯一追溯到该实体

第二章密码学基础

1.密码学的相关概念

密码学分类：

(1)密码编码学:主要研究对信息进行编码，实现信息的隐蔽。常见的“密码学”通常指密码编码学

(2)密码分析学:研究如何分析或破解各种密码、编码体制的一门科学

密码分析也称为密码破译，是指在密码通信过程中，非授权者在不知道密钥的条件下对密文进行分析，试图得到明文或密钥的过程。
主要研究加密消息的破译或消息的伪造。

(3)二者相互独立，又相互依存，在矛盾与斗争中发展，对立统一。

密码分析分类：

image-20220605213440794

(1)唯密文攻击（Ciphertext only）

破译者已知：加密算法、待破译的密文

只知道密文，也就是
[公式]
，那只能通过统计特性分析其中有什么规律了

(2)已知明文攻击（Known plaintext）

破译者已知：加密算法、一定数量的明文和对应的密文

得到了一些给定的明文和对应的密文，在这里可以是
[公式]
的任意非空子集。
攻击人只能得到这些明文及对应的密文，无法自己创建明文或密文

(3)选择明文攻击（Chosen plaintext）

破译者已知：加密算法、选定的明文和对应的密文

除了上面的基础，攻击者还可以任意创造一条明文比如“Excited”，并得到其加密后的密文。
比如用一定的手段渗透Sharon的系统，但是不能直接攻破秘钥，于是只能以她的身份发“Excited”，然后用抓包或者别的方法得到她发送出去的加密文。
攻击人创建一个明文，让Sharon加密，再截获加密后密文，用来统计

(4)选择密文攻击（Chosen ciphertext）

破译者已知：加密算法、选定的密文和对应的明文

除了已知明文攻击的基础，攻击者还可以任意制造或者选择一些密文，并得到其解密后的明文。
比如用一定的手段在通信过程中用伪造密文替换真实密文，然后窃取Sharon获得并解密后的明文，有可能正好发现随手伪造的密文解密结果是有意义的，比如naive。
攻击人创建一个密文，再让Sharon解密，再截获解密后的明文，给自己用来统计

(5)选择文本攻击（Chosen text）

破译者已知：加密算法、选定的明文和对应的密文、选定的密文和对应的明文

可以制造任意明文/密文并得到对应的密文/明文，就是上面两者的结合。

以上攻击强度自上至下由弱到强。选择密文攻击和选择明文攻击的不同之处就是加解密方向不同。

攻击密码体制的常用方法

(1)穷举攻击

(2)统计分析攻击

(3)数学分析攻击

2.密码学加密系统的五元组

明文，密文，密钥，加密算法，解密算法。

3.对加密系统的攻击类型

唯密文攻击（只知道一些密文）
已知明文攻击（知道一些明文与密文对儿）
选择明文攻击（可以用任意明文来得到密文）
选择密文攻击（可以用任意密文得到对应明文）
选择文本攻击（任意明文<->任意密文）

4.kerchkoffs原则

假设攻击者是在已知密码体制的前提下来破译密码系统的密钥
1883年Kerchkoffs第一次明确提出编码原则：

加密算法应建立在算法的公开不影响明文和密钥的安全

实际在我们的网络安全模型中一般假设所有的加密算法都是公开的，密码体系的安全性依赖于秘钥的安全性，秘钥只有发送方和接收方知道，一旦第三方得知这个秘钥，那他们的通信就被攻破了。

这一原则以普遍得到承认，称为判定密码强度的衡量标准，实际上也称为传统密码和现代密码的分界线

Kerchkhoffs假设：

假定：密码分析者知道对方所使用的密码系统
包括明文的统计特性，加密体制（操作方式，处理方法和加/解密算法），密钥空间及统计特性
不知道密钥
成功的密码分析不仅能够恢复出消息明文和密钥，而且能够发现密码体制的弱点，从而控制通信在设计一个密码系统时，目标是在Kerchkhoffs假设的前提下实现安全。

5.两大密码体制

各自的优缺点并分析原因，各自的应用场景

优点/缺点	对称密码	非对称密码
优点	1.算法运算速度较快2.密钥相对较短3.密文明文长度相同	1.密钥分发管理比较简单 2.支持数字签名（解决了不可否认问题）
缺点	1.密钥分发需要安全的通道 2.密钥量大，密钥难于管理 3.难以解决不可否认问题	1.算法复杂，处理速度慢

第三章古典密码体制

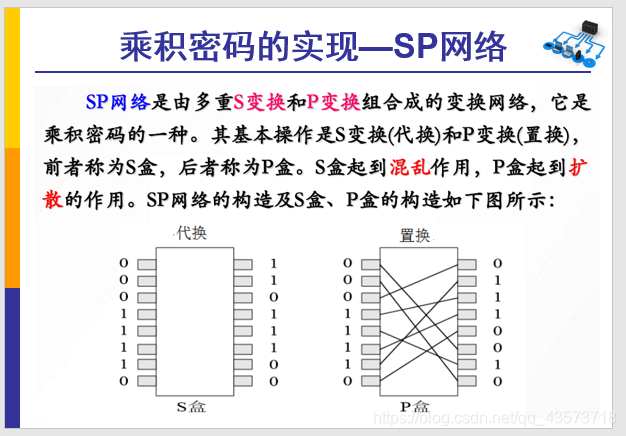
1.理解“代替”和“置换”

置换:只打乱明文的次序

代替:需要用密文来替换掉明文

Playfair置换密码

第一步

编制密码表。在这个5*5的密码表中，共有5行5列字母。将密钥（去除重复字符）从左向右填入,其余按照字母顺序。
密钥是一个单词或词组，若有重复字母，可将后面重复的字母去掉。当然也要把使用频率最少的字母去掉。
如：密钥是Live and learn,去掉后则为liveandr。如果密钥过长可占用第二列或行。

同时字母I和J会被当成一个字母。

如密钥crazy dog，可编制成(按列放入)

C	D	F	M	T
`R`	`O`	H	N	U
`A`	`G`	I ( J )	P	V
`Z`	B	K	Q	W
`Y`	E	L	S	X

第二步

整理明文。将明文每两个字母组成一对。如果成对后有两个相同字母紧挨或最后一个字母是单个的，就插入一个字母X（或者Q）。

如，communist，应成为co,mx,mu,ni,st。

编写密文

对明文加密规则如下：

1 若p1 p2在同一行，对应密文c1 c2分别是紧靠p1 p2 右端的字母。其中第一列被看做是最后一列的右方。

2 若p1 p2在同一列，对应密文c1 c2分别是紧靠p1 p2 下方的字母。其中第一行被看做是最后一行的下方。

3 若p1 p2不在同一行，不在同一列，则c1 c2是由p1 p2确定的矩形的其他两角的字母（至于横向替换还是纵向替换要事先约好，或自行尝试）

密文：KQ SA MF PA OP MF PA

明文：dk ay fn ir mo fn ir

s h i y a

n b c d e

f g j k l

m o p q r

t u v w x

p a与i r形成的矩阵

在这里插入图片描述

Hill密码

在这里插入图片描述

Caesar密码

Caesar是最早的“代替”加密

在这里插入图片描述

对明文p,密文C=(p+k)mod 26，其中k为1~25任意整数

对密文C,明文p=(C-k)mod 26

在这里插入图片描述

维吉尼亚密码

在一个凯撒密码中，字母表中的每一字母都会作一定的偏移，例如偏移量为3时，A就转换为了D、B转换为了E……而维吉尼亚密码则是由一些偏移量不同的恺撒密码组成。

为了生成密码，需要使用表格法。这一表格包括了26行字母表，每一行都由前一行向左偏移一位得到。具体使用哪一行字母表进行编译是基于密钥进行的，在过程中会不断地变换。

image-20220605222403022

例如，假设明文为：

ATTACKATDAWN

选择某一关键词并重复而得到密钥，如关键词为LEMON时，密钥为：

LEMONLEMONLE

对于明文的第一个字母A，对应密钥的第一个字母L，于是使用表格中L行字母表进行加密，得到密文第一个字母L。类似地，明文第二个字母为T，在表格中使用对应的E行进行加密，得到密文第二个字母X。以此类推，可以得到：

明文：ATTACKATDAWN
密钥：LEMONLEMONLE
密文：LXFOPVEFRNHR

解密的过程则与加密相反。例如：根据密钥第一个字母L所对应的L行字母表，发现密文第一个字母L位于A列，因而明文第一个字母为A。密钥第二个字母E对应E行字母表，而密文第二个字母X位于此行T列，因而明文第二个字母为T。以此类推便可得到明文。

优点

一个明文字母可以对应多种密文字母
且每个密文字母使用唯一密钥字母

一次一密

使用与消息一样长且无重复的随机密钥来加密,并且,加密后密钥就丢弃不用

这样的加密是不可攻破的

缺点

产生大规模随机密钥困难
发送与消息等长的密钥本身就不安全

2.能够对使用古典密码加密的密文进行破译

对于Caesar加密，使用穷举攻击，只要对密文进行测试最多25种可能性（将k=1,k=2……依次测试）
对于单表替换加密，使用字母频率或双字母组合频率

第四章分组密码

1.理解分组密码算法如何实现“扩散”和“混乱”的

eg:DES的E盒扩展S盒压缩，一起引起引起雪崩效应

2.S-P网络、雪崩效应

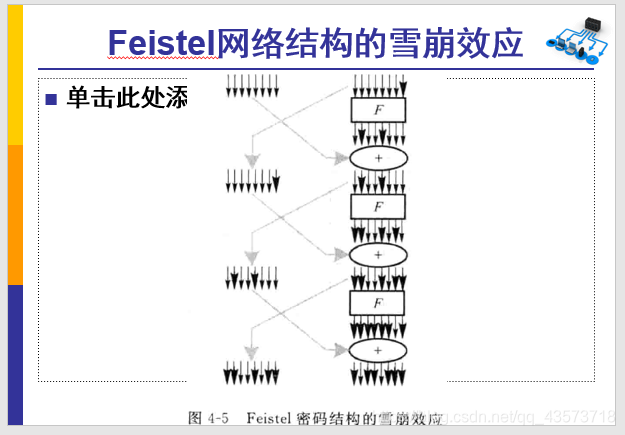
在这里插入图片描述

雪崩效应：

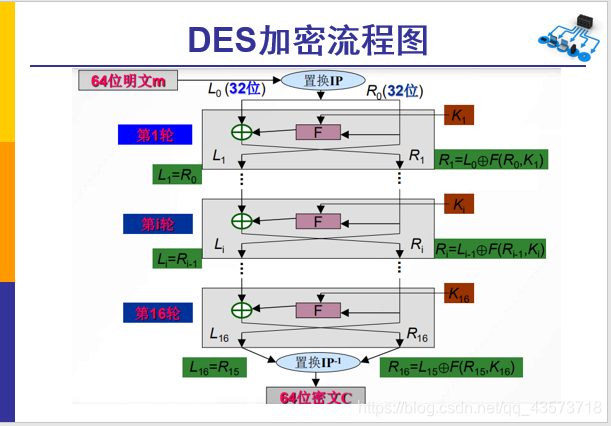
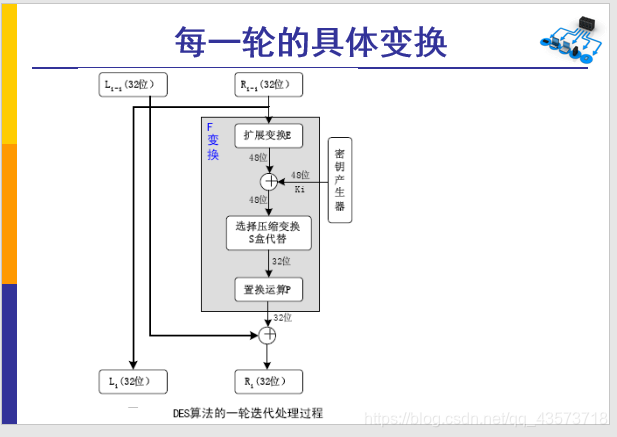
在这里插入图片描述

DES加密流程图

DES加密是“对称密码”算法中的分组加密，与之对应的是流密码：逐个字节就行加密

分组长度：明文和密文为64位分组长度

迭代轮数：每个组合先代换后置换，共16轮

密钥长度：56位（64位-8位奇偶校验位=56位），但存在弱密钥，容易避开。

当n个64位明文数据块经过DES加密后，得到的n个64位密文数据块，将他们串在一起就是密文

image-20220615140620660

image-20220615140627417

步骤一、进行IP置换

image-20220615141212380

例如：58表示，将原来的64位中，第58个放到目前的第1位；后面都按这个规则

步骤二、F轮函数

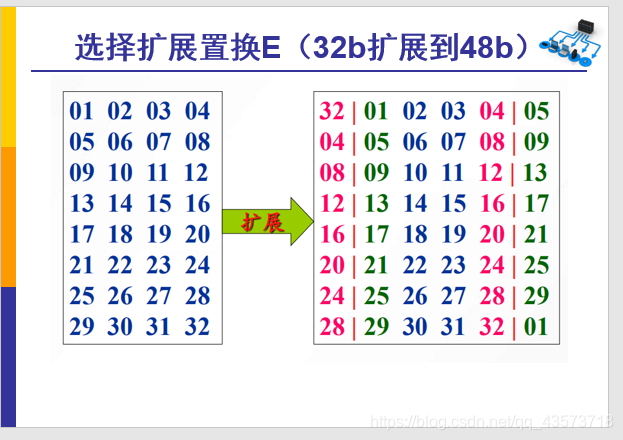
2.1 E扩展

image-20220615141408886

将32位扩展为48位，方法：将32位分成8组，每组4个bit
在每组最前面加上【前一组原始】的第4位。把32位首尾连接，那第一组的最前面，要加上最后一组最后一个bit
在每组最后面加上【后一组原始】的第1位

另一个图，也可以加强解释

image-20220615141758831

2.2 异或

将E扩展出来的48位，与48位密钥进行异或

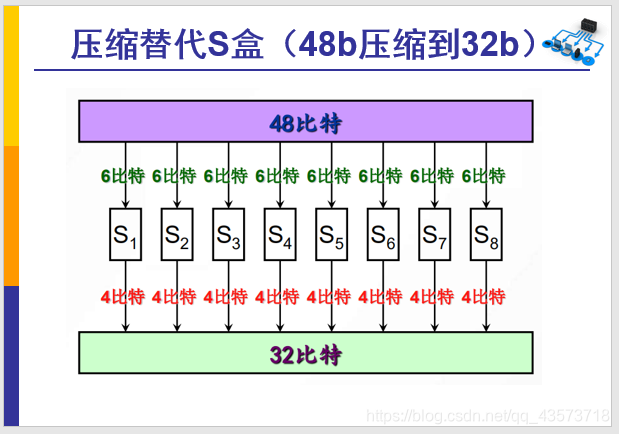
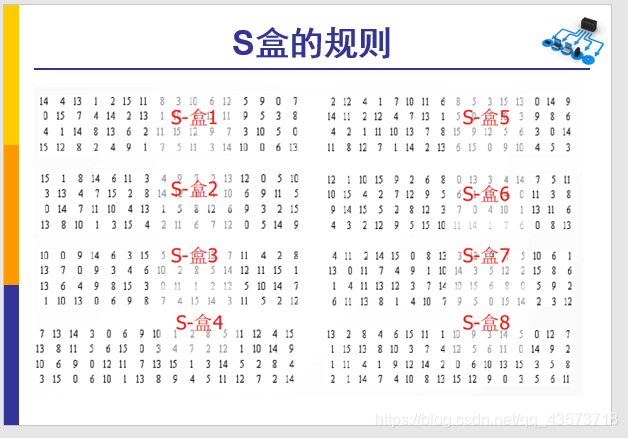
2.3 S盒压缩

直观图

S盒压缩

image-20220615141942964

经过扩展的48位明文和48位密钥进行异或运算后，再使用8个S盒压缩处理得到32位数据。
将48位输入等分为8块，每块6位输入压缩为4位输出

根据下面这个表进行压缩

S盒规则

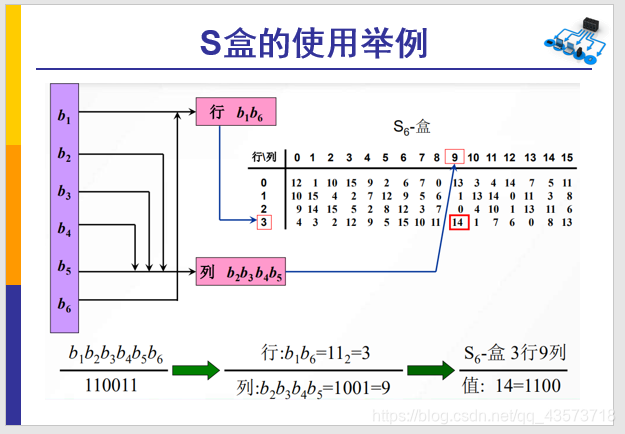
比如

第一组为6个1，将头部和尾部2个1拿出来，再转成10进制，对应结果是3
中间数据也置换成10进制，对应结果是15
3，作为行数；
15，作为列数；
按S1（因为是第1组，一共8组嘛）的第3行，第15列查表，得到13这个结果
再将13，置换成二进制，1101
1101就是最终4bit输出

S盒压缩举例

2.4 P置换

image-20220615142454149

这个P置换和前面的ip置换相近，比如将第16位放到第1位

至此一轮完成，再将P置换的结果与L0进行异或。得到的结果赋值给R1

R1作为下一次的L1

L1（由之前的R0得到）作为下一次参加轮换的参数

经过16次，得到R16与L16，将其拼接后，经过一次逆置换，得到最终结果

在这里插入图片描述

3.DES（分组长度、迭代轮数、密钥长度、S盒、P盒、加密思想）

E盒：（E盒扩展S盒压缩，一起引起引起雪崩效应）

在这里插入图片描述

S盒：（压缩作用）

在这里插入图片描述

P盒：（进行位置置换）(原理：将1~32位的表代换成P盒对应的表)

在这里插入图片描述

4.3DES、AES主要特点

在这里插入图片描述

5.AES的字节代换和列混淆

AES流程图

AES的基本运算：
（1）字节代换（AES的S盒）
（2）行位移
（3）列混淆
（4）轮密钥加

在这里插入图片描述

（1）字节代换（AES的S盒)

功能：将一个字节代换为S表对应的一个新字节

方法：把该字节的高4位作为行值，低4位作为列值

eg:输入字节ox12，查s盒的第ox01行ox02列，得到值oxc9.

在这里插入图片描述

（2）行移位

在这里插入图片描述

列混淆eg:

在这里插入图片描述

（3）列混淆

在这里插入图片描述

（3）轮密钥加

在这里插入图片描述

第六章

1.安全的哈希函数的性质和应用

给定消息x容易计算哈希值单向性抗弱碰撞抗强碰撞性输入任意长度输出固定长度

哈希函数的性质：

1.可用于“任意”长度的消息
2.产生定长的输出
3.对于给定的消息x，计算H（x）比较容易，用于硬件软件均可实现
4.单向性
5.抗弱碰撞性
6.抗强碰撞性

hash 函数的重要应用：
1.数字签名
2.数据完整性的保证
3.安全存储口令
4.快速进行关键字查找

2.MD5和SHA1的主要特点

MD5的主要特点：
输入：最大长度为小于2^64位（2^64 -1位）的消息————>输出：128位消息摘要
处理：输入消息以512比的分组为单位处理

SHA1的主要特点：
输入：最大长度为小于2^64位（2^64 -1位）的消息————>输出：160位消息摘要
处理：输入消息以512比的分组为单位处理

3. 消息认证的目的和方法

消息认证的目的：
1.验证消息的真实性(身份认证)，验证消息的来源是真实的而不是冒充的
2.验证消息的完整性（消息认证），检查消息在传送或存储过程中是否被修改

4.认证函数的三种实现方法

1.基于消息加密的认证
2.基于消息认证码(MAC)的认证
3.基于哈希函数的认证

在这里插入图片描述

5.能够对一个认证协议进行分析

第八章数字签名

1.数字签名要解决的问题

A发送消息给B：A（不可抵赖）——————>B（不可伪造）（不可重用）
(1)不可抵赖 (假如：A可以否认发过该消息，B无法证明A确实发了该消息)
(2)不可伪造 (假如：B伪造一个不同的消息，但声称是从A收到的）
(3)不可重用 (假如：签名没有和消息绑定)

eg:
问题的提出：
普通的报文鉴别能用来保护通信双方免受任何第三方的攻击,
然而, 它无法防止通信双方互相攻击
假定A发送一个经过鉴别的消息给B，双方之间的争议可能有多种形式：
1）B伪造一个不同的消息，但声称是从A收到的
2）A可以否认发过该消息，B无法证明A确实发了该消息
解决以上问题可以用数字签名技术，它是对传统笔迹签名的模拟
传统笔迹签名：
一般认为，传统的手写签名具有以下特点：
1）手写签名是“不可伪造”的
2）手写签名是“不可抵赖”的
3）手写签名是“不可重用”的
数字签名至少应该具有这些能力